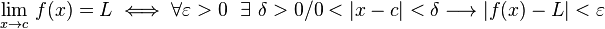Límite 

En matemática, el concepto de límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.

En cálculo infinitesimal (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación,integración, entre otros. Si bien, el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclídeo, es la clase de conjuntos abiertosinducidos por dicha métrica, lo que permite definir rigurosamente la noción de límite.

El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.

Límite de una función

Visualización en un sistema decoordenadas cartesianas de los parámetros utilizados en la definición de límite.

En análisis real para funciones de una variable, se puede hacer una definición de límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo o radio de convergencia se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. El punto c es punto de acumulación del dominio de la función.¹Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos.

Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:

si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.

Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más estricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:

"El límite de f(x) cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε unidades".

Esta definición, se puede escribir utilizando términos lógico-matemáticos y de manera compacta:

Esta definición es equivalente al límite de una sucesión, una función es continua si:

Para la función f(x) = x² - 9/ x - 3 se tiene límite en el punto 3, que no está en el dominio, cuando los valores del dominio se acercan a 3, los valores de la función se aproximan a 6. 3 es un punto de acumulación de D_f²

figura de pentágono 

figura  de  octágono 

figura  decagono 

figura de dodecagono 

figuras de limites  por izquierda y derecha 

Trabajo entregado

CALCULO DIFERENCIAL

Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones. El principal objeto de estudio en el calculo diferencial es la derivada.

EVOLUCION HISTORICA

El cálculo se deriva de la antigua geometría griega. Demócrito calculo el volumen de pirámides y conos, Eudoxo y Arquímedes utilizaron el "método de agotamiento" para encontrar el área de un circulo con la exactitud requerida mediante el uso de polígonos inscritos.

 Isaac Newton fue discípulo de Barrow.

En el siglo XVII, Francesco B. Cavalieri y Evangelista Torricelli ampliaron el uso de los infinitesimales, y Descartes y Pierre de Fermat utilizaron el algebra para encontrar el area y las tangentes (integración y diferenciación en términos modernos). Fermat e Isaac Barrow tenia la certeza de que Gottfried W. Leibniz (hacia 1670) quienes demostraron que son inversos, lo que se conoce como "teorema fundamental del calculo".

En el siglo XVIII aumento considerablemente el numero de aplicaciones del calculo, pero el uso impreciso de las cantidades infinitivas e infinitesimales, así como la intuición geométrica, causaban todavía confusión y controversia sobre sus fundamentos.

En el siglo XIX los analistas matemáticos sustituyeron esas vaguedades por fundamentos solidos basados en cantidades finitas: Bernhard Bolzano y Augustin Loui Cauchy definieron con precisión los límites y las derivadas; Cauchy y Bernhard Riemann hicieron lo propio con las integrales. En el siglo XX, el análisis no convencional, legitimó el uso de los infitesimales. Al mismo tiempo, la aparición de los creadores o computadoras ha incrementado las aplicaciones y velocidad del cálculo. 

USO ANTIGUO DEL CÁLCULO:

En sus comienzos el cálculo fue desarrollado para estudiar cuatro problemas científicos y matemáticos:

1._ Encontrar la tangente a una curva en un punto.

2._ Encontrar el valor máximo o mínimo de una cantidad.

3._ Encontrar la longitud de una curva, en el área de una región y el volumen de un solido.

4._ Dada una formula de la distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar la velocidad y la aceleración del cuerpo en cualquier instante.

ACTUALIDA

El éxito del cálculo ha sido extendido con el tiempo a las ecuaciones diferenciales, al cálculo de vectores, al cálculo de variaciones, al análisis complejo y a la topología algebraica y topología diferencial entre muchas otras ramas. El desarrolló y uso del cálculo ha tenido efectos muy importantes en casi todas las áreas de la vida moderna: es fundamento para el cálculo numérico aplicado en casi todos los campos técnicos y/o científicos cuya principal característica es la continuidad de sus elementos, en especial la física. La capacidad y velocidad de las computadoras hacia el cálculo hacen que humanamente seria imposible hacer millones de operaciones por segundo.

El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial de una función.

El estudio del cambio de una función es de especial interés para el cálculo diferencial, en concreto el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.

Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de  en cada punto . Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.

La inversa de una derivada se llama primitiva, antiderivada o integral indefinida

Diferenciación y diferenciabilidad

Una función de una variable es diferenciable en un punto  si su derivada existe en ese punto; una función es diferenciable en un intervalo si lo es en cada punto  perteneciente al intervalo. Si una función no es continua en c, entonces no puede ser diferenciable en c; sin embargo, aunque una función sea continua en c, puede no ser diferenciable. Es decir, toda función diferenciable en un punto c es continua en c, pero no toda función continua en ces diferenciable en c (como f(x) = |x| es continua pero no diferenciable en x = 0).

Noción de derivada

Artículo principal: Derivada

Recta secante entre los puntosf(x+h) y f(x).

Las derivadas se definen tomando el límite de la pendiente de las rectassecantes conforme se van aproximando a la recta tangente.

Es difícil hallar directamente la pendiente de la recta tangente de una función porque sólo conocemos un punto de ésta, el punto donde ha de ser tangente a la función. Por ello, aproximaremos la recta tangente por rectas secantes. Cuando tomemos el límite de las pendientes de las secantes próximas, obtendremos la pendiente de la recta tangente.

Para obtener estas pendientes, tomemos un número arbitrariamente pequeño que llamaremos h. h representa una pequeña variación en x, y puede ser tanto positivo como negativo. La pendiente de la recta entre los puntos  y  es

Esta expresión es un cociente diferencial de Newton. La derivada de f en x es el límite del valor del cociente diferencial conforme las líneas secantes se acercan más a la tangente:

Si la derivada de f existe en cada punto x, podemos definir la derivada de f como la función cuyo valor en el punto x es la derivada de f en x.

Puesto que la inmediata sustitución de h por 0 da como resultado una división por cero, calcular la derivada directamente puede ser poco intuitivo. Una técnica es simplificar el numerador de modo que la h del denominadorpueda ser cancelada. Esto resulta muy sencillo con funciones polinómicas, pero para la mayoría de las funciones resulta demasiado complicado. Afortunadamente, hay reglas generales que facilitan la diferenciación de la mayoría de las funciones descritas.

El cociente diferencial alternativo

La derivada de f(x) (tal como la definió Newton) se describió como el límite, conforme h se aproxima a cero. Una explicación alternativa de la derivada puede ser interpretada a partir del cociente de Newton. Si se utiliza la fórmula anterior, la derivada en c es igual al límite conforme h se aproxima a cero de [f(c + h) - f(c)] / h. Si se deja que h = x - c(por ende c + h = x), entonces x se aproxima a c (conforme h tiende a cero). Así, la derivada es igual al límite conformex se aproxima a c, de [f(x) - f(c)] / (x - c). Esta definición se utiliza para una demostración parcial de la regla de la cadena.

Funciones de varias variables

Para funciones de varias variables  las condiciones de diferenciabilidad son más estrictas y requieren más condiciones a parte de la existencia de derivadas parciales. En concreto se requiere la existencia de una aproximación lineal a la función en el entorno de un punto. Dada una base vectorial esta aproximación lineal viene dada por la matriz jacobiana:

Historia

Los problemas típicos que dieron origen al cálculo infinitesimal, comenzaron a plantearse en la época clásica de laantigua Grecia (siglo III a.c), con conceptos de tipo geométrico como el problema de la tangente a una curva deApolonio de Perge, pero no se encontraron métodos sistemáticos de resolución hasta el siglo XVII por la obra de Isaac Newton y Gottfried Leibniz.

Ellos sintetizaron dos conceptos y métodos usados por sus predecesores en lo que hoy llamamos «diferenciación» e «integración». Desarrollaron reglas para manipular las derivadas (reglas de derivación) y mostraron que ambos conceptos eran inversos (teorema fundamental del cálculo).

Desde el siglo XVII, muchos matemáticos han contribuido al cálculo diferencial. En el siglo XIX, el cálculo tomó un estilo más riguroso, debido a matemáticos como Augustin Louis Cauchy (1789–1857), Bernhard Riemann (1826–1866), yKarl Weierstrass (1815–1897). Fue también durante este periodo que el cálculo diferencial fue generalizado al espacio euclídeo y el plano complejo.

Aplicaciones importantes del cálculo diferencial

Recta tangente a una función en un punto

La recta tangente a una función f(x) es como se ha visto el límite de las rectas secantes cuando uno de los puntos de corte de la secante con la función se hace tender hacia el otro punto de corte. También puede definirse a la recta tangente como la mejor aproximación lineal a la función en su punto de tangencia, esto es, la recta tangente es la función polinómica de primer grado que mejor aproxima a la función localmente en el punto de tangencia que consideremos.

Si conocemos la ecuación de la recta tangente T_a(x) a la función f(x) en el punto a podemos tomar T_a(x) como una aproximación razonablemente buena de f(x) en las proximidades del punto a. Esto quiere decir que si tomamos un punto a + h y lo evaluamos tanto en la función como en la recta tangente, la diferencia  será despreciable frente a h en valor absoluto si h tiende a cero. Cuanto más cerca estemos del punto a tanto más precisa será nuestra aproximación de f(x).

Para una función f(x) derivable localmente en el punto a, la recta tangente a f(x) por el punto a es:

T_a(x)= f(a) + f '(a)(x-a).

Uso de las derivadas para realizar gráficos de funciones

Las derivadas son una útil herramienta para examinar las gráficas de funciones. En particular, los puntos en el interior de un dominio de una función de valores reales que llevan a dicha función a un extremo local tendrán una primera derivada de cero. Sin embargo, no todos los puntos críticos son extremos locales. Por ejemplo, f(x)=x³ tiene un punto crítico en x=0, pero en ese punto no hay un máximo ni un mínimo. El criterio de la primera derivada y el criterio de la segunda derivada permiten determinar si los puntos críticos son máximos, mínimos o ninguno.

En el caso de dominios multidimensionales, la función tendrá una derivada parcial de cero con respecto a cada dimensión en un extremo local. En este caso, la prueba de la segunda derivada se puede seguir utilizando para caracterizar a los puntos críticos, considerando el eigenvalor de la matriz Hessiana de las segundas derivadas parciales de la función en el punto crítico. Si todos los eigenvalores son positivos, entonces el punto es un mínimo local; si todos son negativos es un máximo local. Si hay algunos eigenvalores positivos y algunos negativos, entonces el punto crítico es un punto silla, y si no se cumple ninguno de estos casos, la prueba es no concluyente (e.g., los engeivalores son 0 y 3).

Una vez que se encuentran los extremos locales, es mucho más fácil hacerse de una burda idea de la gráfica general de la función, ya que (en el caso del dominio mono dimensional) se incrementará o decrementará uniformemente excepto en los puntos críticos, y por ello (suponiendo su continuidad) tendrá valores intermedios entre los valores en los puntos críticos de cada lado.

Aproximación local de Taylor

Hemos visto que podemos aproximar mediante su recta tangente a una función derivable localmente en un punto. Si se cumple que la función es suficientemente suave en el punto o dominio de estudio (esto es, la función es de clase ) se puede aproximar la función no por polinomios de grado uno, sino por polinomios de grado dos, tres, cuatro y sucesivamente. Esta aproximación recibe el nombre de «desarrollo polinómico de Taylor» y se define de la siguiente manera:

Donde P(x) es el polinomio de grado n que mejor aproxima a la función en el punto x=a. Nótese que si evaluamos P(x) en x=a todos los términos salvo el f(a) se anulan, luego P(a) = f(a). Nótese también que la ecuación de la recta tangente del apartado anterior corresponde al caso en el que n=1.

Cuando a=0 el desarrollo se denomina desarrollo de MacLaurin. En la práctica la mayoría de las veces se emplean desarrollos de MacLaurin. Ejemplos de desarrollos importantes de MacLaurin son:

Nótese el símbolo  que denota aproximación que no igualdad. Si la función a aproximar es infinitamente derivable () y agregamos infinitos términos al desarrollo entonces el  se convierte en un  y el desarrollo anterior se convierte en una serie de Taylor. Las funciones que son igual a su serie de Taylor se denominan funciones analíticas.

Cálculo de puntos

Puntos singulares

Se denominan puntos singulares ó estacionarios a los valores de la variable en los que se anula la derivada f '(x) de una función f(x), es decir, si f ´(x)=0 en x₁, x₂, x₃, . . . , x_n, entonces x₁, x₂, x₃, . . . , x_n son puntos singulares de f(x). Los valores f(x₁), f(x₂), f(x₃), . . . , f(x_n), se llaman valores singulares.

Puntos críticos

Por punto crítico se entiende: un punto singular, un punto donde no exista la derivada o un punto extremo a o b del dominio [a,b] de definición de la función.

Si la segunda derivada es positiva en un punto crítico, se dice que el punto es un mínimo local; si es negativa, se dice que el punto es un máximo local; si vale cero, puede ser tanto un mínimo, como un máximo o un punto de inflexión. Derivar y resolver en los puntos críticos es a menudo una forma simple de encontrar máximos y mínimos locales, que pueden ser empleados en optimización. Aunque nunca hay que despreciar los extremos en dichos problemas

Generalización del cálculo diferencial

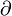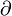Cuando una función depende de más de una variable, se utiliza el concepto de derivada parcial. Las derivadas parciales se pueden pensar informalmente como tomar la derivada de una función con respecto a una de ellas, manteniendo las demás variables constantes. Las derivadas parciales se representan como  (en donde ; es una 'd' redondeada conocida como 'símbolo de la derivada parcial').

El concepto de derivada puede ser extendido de forma más general. El hilo común es que la derivada en un punto sirve como una aproximación lineal a la función en dicho punto. Quizá la situación más natural es que las funciones sean diferenciables en las variedades. La derivada en un cierto punto entonces se convierte en una transformación lineal entre los correspondientes espacios tangentes y la derivada de la función se convierte en un mapeo entre losgrupos tangentes.

Para diferenciar todas las funciones continuas y mucho más, se puede definir el concepto de distribución.

Para las funciones complejas de una variable compleja, la diferenciabilidad es una condición mucho más fuerte que la simple parte real e imaginaria de la función diferenciada con respecto a la parte real e imaginaria del argumento. Por ejemplo, la función  satisface lo segundo, pero no lo primero. Vea también Función holomórfica.

Vea también: diferintegral.

Dadas las funciones, de valor real, y ambas con dominio, el problema consiste en hallar los valores máximos o mínimos (valores extremos) de cuando se restringe a tomar valores en el conjunto

El cálculo diferencial se origina en el siglo XVll, al estudiar la velocidad de los cuerpos al caer al vacío ya que cambia de momento a otro, la velocidad en cada instante debe calcularse.
En1666, el científico ingles Isaac Newton fue el primero en desarrollar métodos matemáticos para resolver problemas de esta índole.
El filosofo y matemático alemán Gottfried Leibniz analizoinvestigaciones similares e ideando símbolos matemáticos que se aplican hasta nuestros días.
Pierre Fermat matemático francés, quien en su obra habla de sus métodos diseñados para determinar los máximos ymínimos.
Dicha obra influencio a Leibniz en la inversión del cálculo diferencial.
Fermat dejo casi todos sus teoremas sin demostrar.
Nicolás Oresme estableció que en la proximidad del punto de una curvaen que la ordenada se considera máxima o mínima, dicha ordenada varía más pausadamente.
Fermat en su estudio de máximo y mínimo, las tangentes y las cuadraturas, igualar a cero la derivada de lafunción, debido a que la tangente a la curva en los puntos en que la función tiene su máximo o su mínimo, es decir, la función es paralela al eje “x” donde la pendiente es la tangente nula.
IsaacNewton por medio del “triangulo característico” en donde la hipotenusa es un arco infinitesimal de curva y sus catetos son incrementos infinitesimales en que difieren las abscisas y las ordenadas de losextremos de arco.
Newton concibió el método de las “fluxiones”, considerando a la curva como la trayectoria de un punto que fluye; denomina “momento” de la cantidad fluente al arco mucho muy cortorecorrido de un tiempo excesivamente pequeño llamado la razón del momento, al tiempo correspondiente, es decir, la velocidad.
“fluente” es la cantidad variable que se identifica como “función”“fluxión” es la velocidad o rapidez de variación, de la fluente que se identifica como “derivada; al incremento infinitesimal o instantáneo de la fluente se le llama “momento” que se identifica como...